Resonance

The following is a LCR series circuit (L stands for inductor, C for capacitor, and R for resistor).

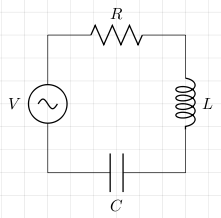
The inductive reactance is

	
XL = ωL
	
      

The capacitive reactance is

	
XC = 1/(ωC)
	
      

The impedance is

	
Z = R +j(XL-XC)
	
      

The impedance is at a minimum when XL=XC which happens when

	
ωL = 1/(ωC)
ω2L = 1/C
ω2 = 1/(LC)
ω = 1/√(LC)
	
      

This is known as the resonant frequency. At this point the instantaneous current is at its maximum and in phase with the instantaneous voltage.

The bandwidth — the range of frequencies either side of ω where the instantaneous current is above the cut-off frequency — is

	
Δω = R/L
	
      

The Q factor gives us an indication of the sharpness of the current peak. A high Q factor is a sharp peak, and a low Q factor is a broad peak. This can be calculated as follows:

	
Q = ωL/R
  = 1/(RωC)     [ωL = 1/(ωC)]
  = 1/R×√(L/C)
	
      

The selectivity of the circuit is given by the Q factor. Also, at the resonant frequency:

	
VC = VL = QV
	
      

References

Fischer-Cripps. A.C., The Electronics Companion. Institute of Physics, 2005.