Inductor
A inductor is a device which induces a voltage when the current through it changes. This ability is called inductance and this is measured in henrys.
Consider the following circuit.
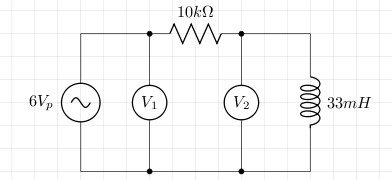
The voltage source is a signal generator which generates a direct current square wave with a 6 volts peak. The voltmeters V1 and V2 are in fact channels 1 and 2 of an oscilloscope. Channel 1 measures the output of the signal generator, and channel 2 measures the voltage across the inductor. The difference between channels 1 and 2 will be the voltage across the resistor. The oscilloscope's screen is shown below where the blue signal is channel 1, yellow is channel 2, and red is the difference between channel 1 and 2.
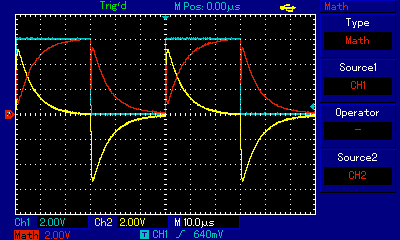
When the blue trace moves from 0 to 6 volts the rate of change of current is controlled by the inductor (L) and the resistor (R). The voltage across the inductor can be calculated with
VL = Ve-Rt/L
In the case of the circuit given earlier and whose measurements are shown on the oscilloscope, L = 0.033, R = 10000, and V = 6.
In the other direction, when the blue trace moves from 6 to 0 volts, then again the rate of change of current is controlled by L and R. In this case, the voltage across the inductor is given by
VL = -Ve-Rt/L
The yellow trace clearly shows us that the voltage across the inductor does not immediately follow the signal generator. When the signal changes from 0 to 6 volts, the magnitude of the opposing, induced, voltage is initially high but then it decreases as the current stabilises. When this induced voltage drops to 0 volts, the current reaches its peak and the the voltage across the inductor is 0 volts and all the voltage is across the resistor. When the signal changes from 6 to 0 volts, the inductor discharges and the voltage across the inductor slowly drops to 0 volts.
Energy is used to create the current through the inductor and this energy is stored in, and released from, the magnetic field. The amount of energy (U) held in the magnetic field at steady current I, is given by the following (i and v are the instantaneous current and voltage respectively):
v = -L di/dt
vi = -Li di/dt (P = iv, and P is Js-1)
|U| = ∫0tLi di/dt di
= L∫0Ii di
= 1/2×LI2
References
Fischer-Cripps. A.C., The Electronics Companion. Institute of Physics, 2005.