Capacitor
A capacitor is a device used to store charge. A capacitor is constructed from two conductors separated by an insulator. The two conductors are usually described as two parallel plates. The ability to store charge is called capacitance and this is measured in farads.
When a voltage is applied across the capacitor's plates, negative charge builds up on one plate and positive charge builds up on the other. Initially, the current is quite large and the voltage very small but as time progresses and the capacitor charges, the current drops and the voltage across the plates increases. If the voltage being applied to the charged capacitor is removed, the the capacitor remains charged due to the coulomb attraction between the charges on the two plates.
Consider the following circuit.
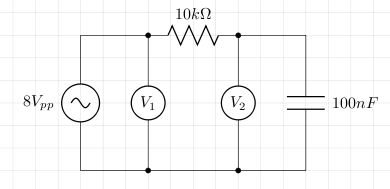
The voltage source is a signal generator which generates a square wave with 8 volts peak to peak. The voltmeters V1 and V2 are in fact channels 1 and 2 of an oscilloscope. Channel 1 measures the output of the signal generator, and channel 2 measures the voltage across the capacitor. The difference between channels 1 and 2 will be the voltage across the resistor and according to Ohm's law, this difference divided by the resistance (10000) gives us the current through the resistor. The oscilloscope's screen is shown below where the blue signal is channel 1, yellow is channel 2, and red is the difference between channels 1 and 2.
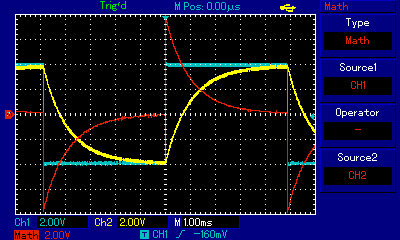
The yellow trace clearly shows the charging and discharging of the capacitor. The red trace shows how the current starts off high (in either direction) then falls to zero as the capacitor charges or discharges.
Energy is used by the voltage source to charge the capacitor. When fully charged, this energy is held in the electric field and it can be released by discharging the capacitor. The amount of energy (U) is given by the following (q and v are the instantaneous charge and voltage respectively):
U = ∫0Qvdq = ∫0Q(q/C)dq [as C = q/v, so v=q/C] = 1/2×Q2/C = 1/2×CV2 [as C=Q/V, so Q=CV]
The following circuit shows three capacitors in series:

In this case:
Q = Q1 = Q2 = Q3 V = V1 + V2 + V3 C = Q/V V1 = Q/C1 V2 = Q/C2 V3 = Q/C3 V = Q(1/C1 + 1/C2 + 1/C3) 1/C = 1/C1 + 1/C2 + 1/C3
The following circuit shows three capacitors in parallel:

In this case:
Q = Q1 + Q2 + Q3 V = V1 = V2 = V3 C = Q/V V1 = Q1/C1 V2 = Q2/C2 V3 = Q3/C3 Q = V1C1 + V2C2 + V3C3 Q = V(C1 + C2 + C3) C = C1 + C2 + C3
References
Fischer-Cripps. A.C., The Electronics Companion. Institute of Physics, 2005.