Function Unit
A function unit comprises an ALU and a shifter.
For its inputs, the function unit takes two values and a function code to select the operation which will be performed upon these values.
These inputs are passed onto the ALU and the shifter.
Internally, there is a multiplexer which selects either the ALU's output or the shifter's output to
be the function unit's output.
The function unit will also output all of the ALU's status bit outputs: C (Carry), V (oVerflow),
N (Negative), and Z (Zero result).
Example
Consider a 16-bit function unit with inputs A and B.
The result output we will call Y.
The following table gives the specification for the function unit. The second column shows the operation performed at the
register transfer level using Verilog notation.
| Function code | Operation |
|---|---|
0000 | Y = A + B |
0001 | Y = A - B |
0010 | Y = A & B |
0011 | Y = A | B |
0100 | Y = A ^ B |
0101 | Y = ~A |
0110 | Y = 0 |
0111 | Y = 0 |
1000 | Y = A |
1001 | Y = A << 1 |
1010 | Y = A >> 1 |
1011 | Undefined |
1100 | Undefined |
1101 | Undefined |
1110 | Undefined |
1111 | Undefined |
The schematic form of the function unit is:
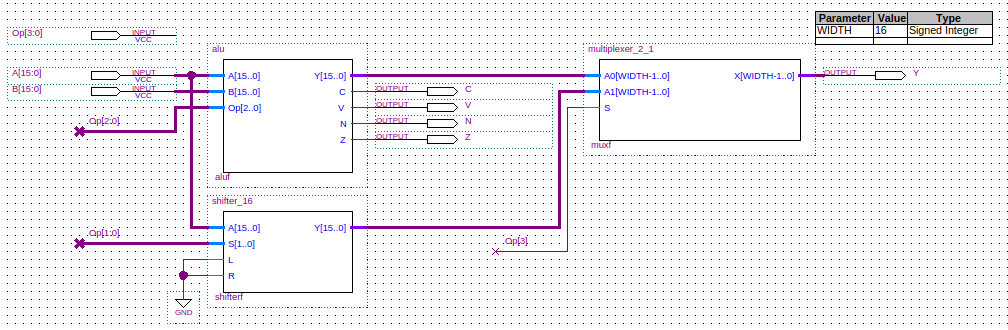
Below is the full Verilog code for the function unit.
module function_unit(Y, C, V, N, Z, A, B, Op);
output [15:0] Y; // Result.
output C; // Carry.
output N; // Negative.
output V; // Overflow.
output Z; // Zero.
input [15:0] A; // Operand.
input [15:0] B; // Operand.
input [3:0] Op; // Operation.
wire [15:0] Ya; // ALU result output.
wire [15:0] Ys; // Shifter result output.
alu aluf(Ya, C, V, N, Z, A, B, {Op[2], Op[1], Op[0]});
shifter_16 shifterf(Ys, A, {Op[1], Op[0]}, 1'b0, 1'b0);
multiplexer_2_1 muxf(Y, Ya, Ys, Op[3]);
endmodule // function_unit
module alu(Y, C, V, N, Z, A, B, Op);
output [15:0] Y; // Result.
output C; // Carry.
output N; // Negative.
output V; // Overflow.
output Z; // Zero.
input [15:0] A; // Operand.
input [15:0] B; // Operand.
input [2:0] Op; // Operation.
wire [15:0] AS, And, Or, Xor, Not;
wire s;
wire Vas;
wire Cas;
// The operations
carry_select_adder_subtractor addsub(AS, Cas, Vas, A, B, Op[0]); // Op == 3'b000, 3'b001
andop aluand(And, A, B); // Op == 3'b010
orop aluor(Or, A, B); // Op == 3'b011
xorop aluxor(Xor, A, B); // Op == 3'b100
notop alunot(Not, A); // Op == 3'b101
multiplexer_8_1 muxy(Y, AS, AS, And, Or, Xor, Not, 16'b0, 16'b0, Op); // Select the result.
nor(s, Op[1], Op[2]); // s == 0 => a logical operation, otherwise and arithmetic operation.
and(C, Cas, s);
and(V, Vas, s);
and(N, Y[15], s); // Most significant bit is the sign bit in 2's complement.
zero z(Z, Y); // All operations can set the Zero status bit.
endmodule // alu
module andop(Y, A, B);
output [15:0] Y; // Result.
input [15:0] A; // Operand.
input [15:0] B; // Operand.
and(Y[0], A[0], B[0]);
and(Y[1], A[1], B[1]);
and(Y[2], A[2], B[2]);
and(Y[3], A[3], B[3]);
and(Y[4], A[4], B[4]);
and(Y[5], A[5], B[5]);
and(Y[6], A[6], B[6]);
and(Y[7], A[7], B[7]);
and(Y[8], A[8], B[8]);
and(Y[9], A[9], B[9]);
and(Y[10], A[10], B[10]);
and(Y[11], A[11], B[1]);
and(Y[12], A[12], B[12]);
and(Y[13], A[13], B[13]);
and(Y[14], A[14], B[14]);
and(Y[15], A[15], B[15]);
endmodule // andop
module orop(Y, A, B);
output [15:0] Y; // Result.
input [15:0] A; // Operand.
input [15:0] B; // Operand.
or(Y[0], A[0], B[0]);
or(Y[1], A[1], B[1]);
or(Y[2], A[2], B[2]);
or(Y[3], A[3], B[3]);
or(Y[4], A[4], B[4]);
or(Y[5], A[5], B[5]);
or(Y[6], A[6], B[6]);
or(Y[7], A[7], B[7]);
or(Y[8], A[8], B[8]);
or(Y[9], A[9], B[9]);
or(Y[10], A[10], B[10]);
or(Y[11], A[11], B[1]);
or(Y[12], A[12], B[12]);
or(Y[13], A[13], B[13]);
or(Y[14], A[14], B[14]);
or(Y[15], A[15], B[15]);
endmodule // orop
module xorop(Y, A, B);
output [15:0] Y; // Result.
input [15:0] A; // Operand.
input [15:0] B; // Operand.
xor(Y[0], A[0], B[0]);
xor(Y[1], A[1], B[1]);
xor(Y[2], A[2], B[2]);
xor(Y[3], A[3], B[3]);
xor(Y[4], A[4], B[4]);
xor(Y[5], A[5], B[5]);
xor(Y[6], A[6], B[6]);
xor(Y[7], A[7], B[7]);
xor(Y[8], A[8], B[8]);
xor(Y[9], A[9], B[9]);
xor(Y[10], A[10], B[10]);
xor(Y[11], A[11], B[1]);
xor(Y[12], A[12], B[12]);
xor(Y[13], A[13], B[13]);
xor(Y[14], A[14], B[14]);
xor(Y[15], A[15], B[15]);
endmodule // xorop
module notop(Y, A);
output [15:0] Y; // Result.
input [15:0] A; // Operand.
not(Y[0], A[0]);
not(Y[1], A[1]);
not(Y[2], A[2]);
not(Y[3], A[3]);
not(Y[4], A[4]);
not(Y[5], A[5]);
not(Y[6], A[6]);
not(Y[7], A[7]);
not(Y[8], A[8]);
not(Y[9], A[9]);
not(Y[10], A[10]);
not(Y[11], A[11]);
not(Y[12], A[12]);
not(Y[13], A[13]);
not(Y[14], A[14]);
not(Y[15], A[15]);
endmodule // notop
module zero(Z, A);
output Z; // Result.
input [15:0] A; // Operand.
wire [15:0] Y; // Temp result.
xnor(Y[0], A[0], 0);
xnor(Y[1], A[1], 0);
xnor(Y[2], A[2], 0);
xnor(Y[3], A[3], 0);
xnor(Y[4], A[4], 0);
xnor(Y[5], A[5], 0);
xnor(Y[6], A[6], 0);
xnor(Y[7], A[7], 0);
xnor(Y[8], A[8], 0);
xnor(Y[9], A[9], 0);
xnor(Y[10], A[10], 0);
xnor(Y[11], A[11], 0);
xnor(Y[12], A[12], 0);
xnor(Y[13], A[13], 0);
xnor(Y[14], A[14], 0);
xnor(Y[15], A[15], 0);
and(Z, Y[0], Y[1], Y[2], Y[3], Y[4],
Y[5], Y[6], Y[7], Y[8],
Y[9], Y[10], Y[11], Y[12],
Y[13], Y[14], Y[15]);
endmodule // zero
module carry_select_adder_subtractor(S, C, V, A, B, Op);
output [15:0] S; // The 16-bit sum/difference.
output C; // The 1-bit carry/borrow status.
output V; // The 1-bit overflow status.
input [15:0] A; // The 16-bit augend/minuend.
input [15:0] B; // The 16-bit addend/subtrahend.
input Op; // The operation: 0 => Add, 1=>Subtract.
wire C15; // The carry out bit of adder/subtractor, used to generate final carry/borrrow.
wire [15:0] Bx;
// Looking at the truth table for not we see that
// B xor 0 = B, and
// B xor 1 = not(B).
// So, if Op==1 means we are subtracting, then
// adding A and B xor Op alog with setting the first
// carry bit to Op, will give us a result of
// A+B when Op==0, and A+not(B)+1 when Op==1.
// Note that not(B)+1 is the 2's complement of B, so
// this gives us subtraction.
xor(Bx[0], B[0], Op);
xor(Bx[1], B[1], Op);
xor(Bx[2], B[2], Op);
xor(Bx[3], B[3], Op);
xor(Bx[4], B[4], Op);
xor(Bx[5], B[5], Op);
xor(Bx[6], B[6], Op);
xor(Bx[7], B[7], Op);
xor(Bx[8], B[8], Op);
xor(Bx[9], B[9], Op);
xor(Bx[10], B[10], Op);
xor(Bx[11], B[11], Op);
xor(Bx[12], B[12], Op);
xor(Bx[13], B[13], Op);
xor(Bx[14], B[14], Op);
xor(Bx[15], B[15], Op);
xor(C, C15, Op); // Carry = C15 for addition, Carry = not(C15) for subtraction.
carry_select_adder csa(S, C15, V, A, Bx, Op);
endmodule // carry_select_adder_subtractor
module carry_select_adder(S, C, V, A, B, Cin);
output [15:0] S; // The 16-bit sum.
output C; // The 1-bit carry.
output V; // The 1-bit overflow status.
input [15:0] A; // The 16-bit augend.
input [15:0] B; // The 16-bit addend.
input Cin; // The initial carry in.
wire [3:0] S1_0; // Nibble 1 sum output with carry input 0.
wire [3:0] S1_1; // Nibble 1 sum output with carry input 1.
wire [3:0] S2_0; // Nibble 2 sum output with carry input 0.
wire [3:0] S2_1; // Nibble 2 sum output with carry input 1.
wire [3:0] S3_0; // Nibble 3 sum output with carry input 0.
wire [3:0] S3_1; // Nibble 3 sum output with carry input 1.
wire C1_0; // Nibble 1 carry output with carry input 0.
wire C1_1; // Nibble 1 carry output with carry input 1.
wire C2_0; // Nibble 2 carry output with carry input 0.
wire C2_1; // Nibble 2 carry output with carry input 1.
wire C3_0; // Nibble 3 carry output with carry input 0.
wire C3_1; // Nibble 3 carry output with carry input 1.
wire C0; // Nibble 0 carry output used to select multiplexer output.
wire C1; // Nibble 1 carry output used to select multiplexer output.
wire C2; // Nibble 2 carry output used to select multiplexer output.
wire V0; // Nibble 0 overflow output.
wire V1_0; // Nibble 1 overflow output with carry input 0.
wire V1_1; // Nibble 1 overflow output with carry input 1.
wire V2_0; // Nibble 2 overflow output with carry input 0.
wire V2_1; // Nibble 2 overflow output with carry input 1.
wire V3_0; // Nibble 3 overflow output with carry input 0.
wire V3_1; // Nibble 3 overflow output with carry input 1.
ripple_carry_adder rc_nibble_0(S[3:0], C0, V0, A[3:0], B[3:0], Cin); // Calculate S nibble 0.
ripple_carry_adder rc_nibble_1_carry_0(S1_0, C1_0, V1_0, A[7:4], B[7:4], 0); // Calculate S nibble 1 with carry input 0.
ripple_carry_adder rc_nibble_1_carry_1(S1_1, C1_1, V1_1, A[7:4], B[7:4], 1); // Calculate S nibble 1 with carry input 1.
ripple_carry_adder rc_nibble_2_carry_0(S2_0, C2_0, V2_0, A[11:8], B[11:8], 0); // Calculate S nibble 2 with carry input 0.
ripple_carry_adder rc_nibble_2_carry_1(S2_1, C2_1, V2_1, A[11:8], B[11:8], 1); // Calculate S nibble 2 with carry input 1.
ripple_carry_adder rc_nibble_3_carry_0(S3_0, C3_0, V3_0, A[15:12], B[15:12], 0); // Calculate S nibble 3 with carry input 0.
ripple_carry_adder rc_nibble_3_carry_1(S3_1, C3_1, V3_1, A[15:12], B[15:12], 1); // Calculate S nibble 3 with carry input 1.
multiplexer_2_1 #(1) muxc1(C1, C1_0, C1_1, C0); // C0 selects the carry output for nibble 1.
multiplexer_2_1 #(1) muxc2(C2, C2_0, C2_1, C1); // C1 selects the carry output for nibble 2.
multiplexer_2_1 #(1) muxc(C, C3_0, C3_1, C2); // C2 selects the carry output for nibble 3 which is the global carry output.
multiplexer_2_1 #(1) muxv(V, V3_0, V3_1, C2); // C2 selects the overflow output for nibble 3 which is the global overflow output.
multiplexer_2_1 #(4) muxs1(S[7:4], S1_0, S1_1, C0); // C0 selects the result for nibble 1.
multiplexer_2_1 #(4) muxs2(S[11:8], S2_0, S2_1, C1); // C1 selects the result for nibble 2.
multiplexer_2_1 #(4) muxs3(S[15:12], S3_0, S3_1, C2); // C2 selects the result for nibble 3.
endmodule // carry_select_adder
module ripple_carry_adder(S, C, V, A, B, Cin);
output [3:0] S; // The 4-bit sum.
output C; // The 1-bit carry.
output V; // The 1-bit overflow status.
input [3:0] A; // The 4-bit augend.
input [3:0] B; // The 4-bit addend.
input Cin; // The carry input.
wire C0; // The carry out bit of fa0, the carry in bit of fa1.
wire C1; // The carry out bit of fa1, the carry in bit of fa2.
wire C2; // The carry out bit of fa2, the carry in bit of fa3.
full_adder fa0(S[0], C0, A[0], B[0], Cin); // Least significant bit.
full_adder fa1(S[1], C1, A[1], B[1], C0);
full_adder fa2(S[2], C2, A[2], B[2], C1);
full_adder fa3(S[3], C, A[3], B[3], C2); // Most significant bit.
xor(V, C, C2); // Overflow
endmodule // ripple_carry_adder
module full_adder(S, Cout, A, B, Cin);
output S;
output Cout;
input A;
input B;
input Cin;
wire w1;
wire w2;
wire w3;
wire w4;
xor(w1, A, B);
xor(S, Cin, w1);
and(w2, A, B);
and(w3, A, Cin);
and(w4, B, Cin);
or(Cout, w2, w3, w4);
endmodule // full_adder
module multiplexer_2_1(X, A0, A1, S);
parameter WIDTH=16; // How many bits wide are the lines
output [WIDTH-1:0] X; // The output line
input [WIDTH-1:0] A1; // Input line with id 1'b1
input [WIDTH-1:0] A0; // Input line with id 1'b0
input S; // Selection bit
assign X = (S == 1'b0) ? A0 : A1;
endmodule // multiplexer_2_1
module multiplexer_4_1(X, A0, A1, A2, A3, S1, S0);
parameter WIDTH=16; // How many bits wide are the lines
output [WIDTH-1:0] X; // The output line
input [WIDTH-1:0] A3; // Input line with id 2'b11
input [WIDTH-1:0] A2; // Input line with id 2'b10
input [WIDTH-1:0] A1; // Input line with id 2'b01
input [WIDTH-1:0] A0; // Input line with id 2'b00
input S0; // Least significant selection bit
input S1; // Most significant selection bit
assign X = (S1 == 0
? (S0 == 0
? A0 // {S1,S0} = 2'b00
: A1) // {S1,S0} = 2'b01
: (S0 == 0
? A2 // {S1,S0} = 2'b10
: A3)); // {S1,S0} = 2'b11
endmodule // multiplexer_4_1
module multiplexer_8_1(X, A0, A1, A2, A3, A4, A5, A6, A7, S);
parameter WIDTH=16; // How many bits wide are the lines
output [WIDTH-1:0] X; // The output line
input [WIDTH-1:0] A7; // Input line with id 3'b111
input [WIDTH-1:0] A6; // Input line with id 3'b110
input [WIDTH-1:0] A5; // Input line with id 3'b101
input [WIDTH-1:0] A4; // Input line with id 3'b100
input [WIDTH-1:0] A3; // Input line with id 3'b011
input [WIDTH-1:0] A2; // Input line with id 3'b010
input [WIDTH-1:0] A1; // Input line with id 3'b001
input [WIDTH-1:0] A0; // Input line with id 3'b000
input [2:0] S;
assign X = (S[2] == 0
? (S[1] == 0
? (S[0] == 0
? A0 // {S2,S1,S0} = 3'b000
: A1) // {S2,S1,S0} = 3'b001
: (S[0] == 0
? A2 // {S2,S1,S0} = 3'b010
: A3)) // {S2,S1,S0} = 3'b011
: (S[1] == 0
? (S[0] == 0
? A4 // {S2,S1,S0} = 3'b100
: A5) // {S2,S1,S0} = 3'b101
: (S[0] == 0
? A6 // {S2,S1,S0} = 3'b110
: A7))); // {S2,S1,S0} = 3'b111
endmodule // multiplexer_8_1
module shifter_16(Y, A, S, L, R);
output [15:0] Y; // The shifted result.
input [15:0] A; // The value to be shifted.
input [1:0] S; // The direction of the shift.
input L; // The leftmost bit to shift in.
input R; // The rightmost bit to shift in.
multiplexer_4_1 #(1) mux0(Y[0], A[0], A[1], L, 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux1(Y[1], A[1], A[2], A[0], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux2(Y[2], A[2], A[3], A[1], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux3(Y[3], A[3], A[4], A[2], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux4(Y[4], A[4], A[5], A[3], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux5(Y[5], A[5], A[6], A[4], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux6(Y[6], A[6], A[7], A[5], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux7(Y[7], A[7], A[8], A[6], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux8(Y[8], A[8], A[9], A[7], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux9(Y[9], A[9], A[10], A[8], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux10(Y[10], A[10], A[11], A[9], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux11(Y[11], A[11], A[12], A[10], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux12(Y[12], A[12], A[13], A[11], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux13(Y[13], A[13], A[14], A[12], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux14(Y[14], A[14], A[15], A[13], 1'b0, S[1], S[0]);
multiplexer_4_1 #(1) mux15(Y[15], A[15], R, A[14], 1'b0, S[1], S[0]);
endmodule // shifter_16
The function unit gave the following waveform when test inputs were given:

References
Mano, M. Morris, and Kime, Charles R. Logic and Computer Design Fundamentals. 2nd Edition. Prentice Hall, 2000.