Comparator

A comparator is used to compare two bit sequences bit by bit. A basic comparator will output 1 if both bit sequences are the same. A magnitude comparator will interpret the bit sequences as numbers, say A and B, and may generate different outputs depending on whether A = B, A < B, or A > B.

If we take a 2-bit basic comparator with inputs A (with bits A1 A0) and B (with bits B1 B0) and define the outputs E to be 1 if A = B, then we have the following truth table

From this we can generate the Boolean equation E = ((A0 and B0) or (not(A0) and not(B0))) and ((A1 and B1) or (not(A1) and not(B1))). If we use the exclusive-nor operator (xnor), then this can be written much more simply as: E = (A1 xnor B1) and (A0 xnor B0). This can be generalised for an N-bit basic comparator as follows: E = (AN xnor BN) and ... and (A1 xnor B1) and (A0 xnor B0).

Schematic

We can realise the basic comparator with logic gates as follows:

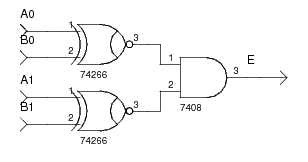
Verilog

Below is the Verilog code for a structural model of a 2-bit basic comparator:

module two_bit_basic_comparator(E, A, B);
   output E;
   input [1:0] A;
   input [1:0] B;
   wire        e0;
   wire        e1;
   
   xnor(e1, A[1], B[1]);
   xnor(e0, A[0], B[0]);
   and(E, e1, e0);
endmodule
         

References

Kleitz, W. Digital Microprocessor Fundamentals. 3rd Edition. Prentice Hall, 2000.