Low Pass Filter

The low pass filter attenuates high frequencies and lets low frequencies through. The basic circuit using a resistor and a capacitor is as follows:

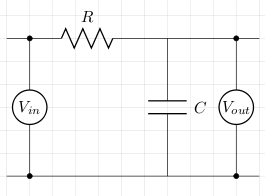
Let X_C be the capacitive reactance and ω be the angular frequency. To calculate the cut-off frequency we proceed as follows:

Vin = IZ = I√(R2+XC2)
Vout = IXC
Vout/Vin = 1/(ωC√(R2+(1/(ω2C2)))) [multiply top and bottom by ωC]
   = 1/√(1+R2ω2C2)   
      

Now, at the cut-off frequency,

1/√2 = 1/√(1+R2ω2C2)
1/2 = 1/(1+R2ω2C2)
1 = R2ω2C2 = RωC
      

Example

Taking a 1kΩ resistor and 100nF capacitor we can calculate ω at the cut-off frequency which will give us the cut-off frequency, f, when we divide that by 2π. So,

C = 100nF = 1×10-7
R = 1kΩ = 1×103
RC = 1×10-4
ω = 1/RC = 1×104
f = ω/2π = 1.590kHz
      

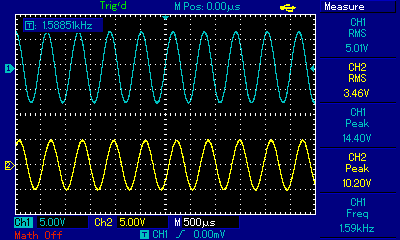
The circuit was built and both V_in and V_out were measured with an oscilloscope at various frequencies. V_in was supplied by a signal generator. The first measurement was taken at roughly the cut-off frequency of 1.59kHz. In the image below, channel 1 (blue trace) is V_in and the channel 2 (yellow trace) is V_out. As expected, V_out/V_in is roughly 0.7.

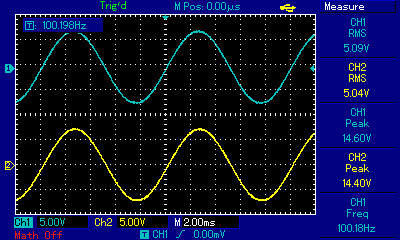
The next measurement was taken at a frequency of roughly 100Hz which is much lower than the cut-off frequency of 1.59kHz. As expected, V_out/V_in is roughly 1. This low frequency signal is passing through the filter.

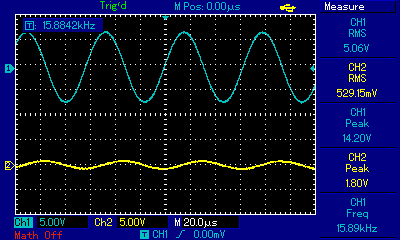
The last measurement was taken at a frequency of roughly 15.9kHz which is much higher than the cut-off frequency of 1.59kHz. As expected, V_out/V_in shows us that the signal has been attenuated.

References

Fischer-Cripps. A.C., The Electronics Companion. Institute of Physics, 2005.