State Diagram
A state diagram shows the current state, inputs, next state, and outputs of a sequential logic circuit in a graphical form. It shows the same information as can be found in a state table.
Example 1
Consider the following Mealy model sequential logic circuit containing a single D flip-flop (not all connections are shown to keep the schematic simple):
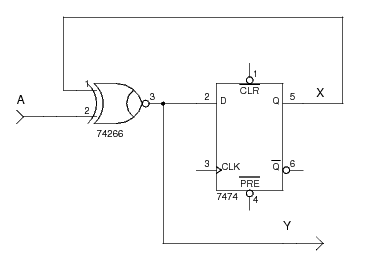
The sole input is A and the sole output is Y.
With one flip-flop we have two (21=2) different states (X=0 and X=1).
We can write the flip-flop input equation for the D flip-flop with output X as:
DX = A xnor X.
The Boolean equation for the output is Y = A xnor X.
Using these we can create the following table:
| Current State | Input | Next State | Output |
|---|---|---|---|
X |
A |
X |
Y |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
The equivalent state diagram is as follows:

The nodes are marked with the circuit states and the edges are marked A/B which mean "input A"
and "output B".
So, in state 0, if we have input 0 then we generate output 1 and move to state 1.
This coincides with the first row of the state table.
Example 2
Consider the following Moore model sequential logic circuit containing a single D flip-flop (not all connections are shown to keep the schematic simple):
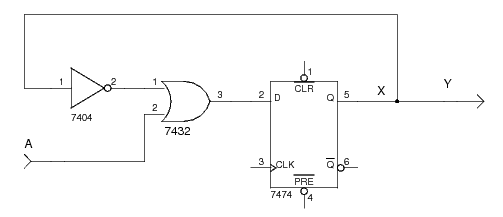
The sole input is A and the sole output is Y.
With one flip-flop we have two (21=2) different states (X=0 and X=1).
We can write the flip-flop input equation for the D flip-flop with output X as:
DX = A or not(X).
The Boolean equation for the output is Y = X.
Using these we can create the following table:
| Current State | Input | Next State | Output |
|---|---|---|---|
X |
A |
X |
Y |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
The equivalent state diagram is as follows:

The nodes are marked with the circuit states and their outputs. The edges between states are marked with the inputs.
So, in state 0, we always generate output 0
and if we have input 0 or 1, then we move to state 1.
This coincides with the first two rows of the state table.
References
Mano, M. Morris, and Kime, Charles R. Logic and Computer Design Fundamentals. 2nd Edition. Prentice Hall, 2000.