Impedance

Impedance is the opposition to an ac current.

Series circuit

In a series circuit, impedance is the vector sum of resistance and reactance (capacitive reactance, inductive reactance). Let Z be the impedance, V the peak or root mean square (RMS) voltage as a vector, and I be the peak or RMS current as a vector. Then

	
Z = V/I
	
      

As in the notes for LCR series circuit, let the peak or RMS voltage through a resistor be VR, the peak or RMS voltage across an inductor be VL, and the peak or RMS voltage across the capacitor be VC. The total peak or RMS voltage, VT, can calculated as shown below

	
|VT| = √(|VR|2+|VL-VC|2)
|VT|/|I| = √(|VR|2/|I|2+|VL/I-VC/I|2)
	
      

From the notes on capacitive reactance, XC, inductive reactance, XL, and Ohm's law, we have

	
XC = VC/I
XL = VL/I
R = VR/I
	
      

So

	
|VT|/|I| = √(|VR|2/|I|2+|VL/I-VC/I|2)
         = √(R2+|XL-XC|2)
|Z|      = √(R2+|XL-XC|2)
	
      

Note that using complex numbers, we can write:

	
V = VR+j(VL-VC)
Z = V/I 
  = VR/I+j(VL-VC)/I
  = R+j(XL-XC)
  = R +j(ωL-1/(ωC))
      
    

For the phase, i.e. difference between the maximum current and voltage, we have:

	
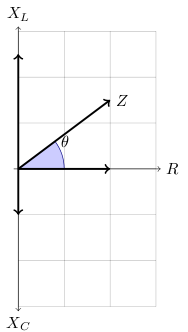
tan θ = (XL-XC)/R	 
	
      

In a RC series circuit, XL=0, gives

	
tan θ = -XC/R
      = -1/(RωC)	 
	
      

In a RL series circuit, XC=0, gives

	
tan θ = XL/R
      = ωL/R
	
      

A LCR circuit is

• capacitively reactive if XC>XL
• inductively reactive if XC<XL
• resonant if XC=XL

References

Fischer-Cripps. A.C., The Electronics Companion. Institute of Physics, 2005.