Feistel Cipher

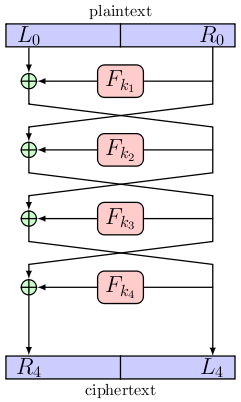
A Feistel cipher/Feistel network is a class of block cipher which comprises several identical rounds, each round constructed from a function and a a swap.

The input block is split in the middle to give to equal sized sub-blocks. Let us call the initial left-hand side sub-block L₀, and the initial right-hand side sub-block R₀. Let the function F_{k_i} be the round function which uses the i^th round key, k_i. These round keys are generated by the key schedule which is unspecified. If we have r rounds, then for 1≤i<r

	
L_i = R_i-1
R_i = L_i-1⊕F_{k_i}(R_i-1)

and for i=r

	
L_r = R_r-1⊕F_{k_r}(L_r-1)
R_r = L_r-1

The figure below shows a Feistel network with four rounds being used to encrypt a plaintext message.

The process of decryption is identical to the one for encryption as long as the round keys are used in reverse order. The figure below shows decryption.

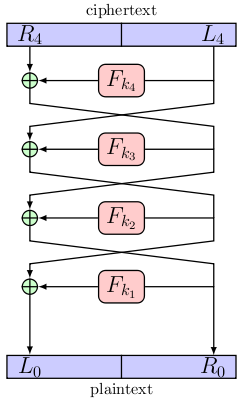
When compared to a substitution/permutation network we see that the Feistel network has an advantage in that it does not require that the round function have an inverse.

References

L. R. Knudsen, M. J. B. Robshaw, The Block Cipher Companion. Springer, 2011.