Graphs

There are two types of graphs: directed and undirected.

directed

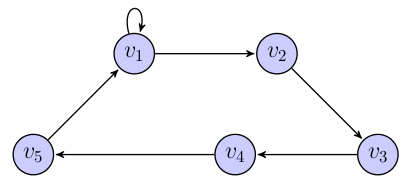
A directed graph is a pair (V,E) such that V is a finite set of vertices and E is a binary relation on V. The set E is called the set of edges. The diagram below shows the directed graph ({v1,v2,v3,v4,v5},{(v1,v1),(v1,v2),(v2,v3),(v3,v4),(v4,v5),(v5,v1)})

undirected

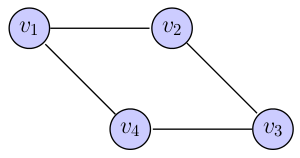
An undirected graph, like the directed type, is a pair (V,E) such that V is a finite set of vertices and E is a binary relation on V, but, the relation E is reflexive. The diagram below shows the directed graph ({v1,v2,v3,v4},{(v1,v2),(v2,v3),(v3,v4),(v4,v1)})

If sEt then we say that the vertex s is adjacent to the vertex t. In the case of a directed graph, we sometimes say that (s,t) is incident from s and incident to t. In the case of an undirected graph, the degree of a vertex s is the number of edges incident on it, i.e. the number of vertices t such that sEt∨tEs. If the out-degree of a vertex in a directed graph is the number or edges leaving it, and the in-degree of that vertex is the number or edges entering it, then the degree of a vertex in a directed graph is the sum of the in-degree and the out-degree.

A path is a sequence of vertices s0,s1,...,sn such that for each two nodes in the sequence si,si+1, siEsi+1. We say that the path is from s0 to sn. The path relation can be seen as the reflexive transitive closure of E, i.e. E* A subpath is a contiguous subsequence of a path, so si,...,sj such that 0≤i<j≤n is a subpath of s0,s1,...,sn. A path is simple if no two vertices in the path are equal. A cycle is a path s0,s1,...,sn where s0=sn. A graph is acyclic if it contains no cycles.

An undirected graph is connected if for every pair of vertices there is exists a path that connects them. The path relation forms equivalence classes of vertices in an undirected graph and these classes are known as connected components. For a directed graph, the term strongly connected is used to describe a graph if for every pair of vertices there is exists a path that connects them. Vertices in a directed graph which are mutually reachable form an equivalence class known as strongly connected components.

Two graphs are said to be isomorphic if an isomorphism exists between them.

The graph (V1,E1) is a subgraph of (V2,E2) if V1⊆V2 and E1⊆E2. Say we have a graph (V2,E2) and a set of vertices V1⊆V2, then the graph (V1,{(s,t)|sE2t}) is a subgraph induced by V1.

A vertex s is the neighbour of vertex t if s is adjacent to t or vice versa.

A bipartite graph (V,E) is an undirected graph such that there is a partition on the set V giving V1 and V2 such that for each edge sEt, either s∈V1∧t∈V2 or s∈V2∧t∈V1.

References

T. H. Cormen, C. E. Leiserson, R. L. Rivest, Introduction to Algorithms. MIT Press, 1990.