Big Theta Notation

The big theta notation is used to describe the asymptotic efficiency of algorithms. It is written Θ(f(n)) where n∈N (sometimes sets other than the set of natural numbers, N, are used).

The expression Θ(f(n)) is the set of functions {g(n):∃c1,c2,n0∈N, ∀n≥n0, 0≤c1f(n)≤g(n)≤c2f(n)}. In plain English, this set is populated by functions that are sandwiched by c1f(n) and c2f(n). This is known as a tight asymptotic bound. For set membership, we write h(n)=Θ(f(n)) and not h(n)∈Θ(f(n)).

Examples

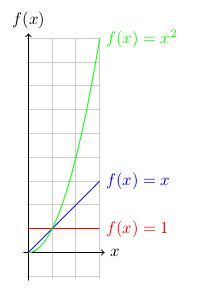
A list of expressions and their big theta bounds are given below, and below this list is a graph showing the growth of some functions.

• 2=Θ(1)
• 4x+2=Θ(x)
• 3x2+4x+2=Θ(x2)

References

T. H. Cormen, C. E. Leiserson, R. L. Rivest, Introduction to Algorithms. MIT Press, 1990.