Big Omega Notation

The big omega notation is used to describe the asymptotic efficiency of algorithms. It is written Ω(f(n)) where n∈N (sometimes sets other than the set of natural numbers, N, are used).

The expression Ω(f(n)) is the set of functions {g(n):∃c,n0∈N, ∀n≥n0, 0≤cf(n)≤g(n)}. In plain English, this set is populated by functions that are bounded cf(n). This is known as an asymptotic lower bound. For set membership, we write h(n)=Ω(f(n)) and not h(n)∈Ω(f(n)).

Examples

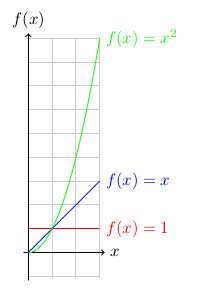
A list of expressions and their big omega bounds are given below, and below this list is a graph showing the growth of some functions.

• 2=Ω(1)
• 4x+2=Ω(x)
• 3x2+4x+2=Ω(x2)

References

T. H. Cormen, C. E. Leiserson, R. L. Rivest, Introduction to Algorithms. MIT Press, 1990.