Thevenin's Theorem

Thevenin's theorem states that any two terminal voltage source can be represented by a single voltage source with internal resistance R_int as in the circuit below:

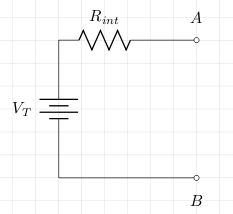
The values for V_T and R_int can either be calculated or measured.

Calculation

When calculating, first use Kirchhoff's or superposition to compute the open circuit voltage V_T. Next calculate the value of R_int by replacing all voltage sources by their internal resistances.

Measuring

To measure, first find the short circuit current from A to B and call this I_SC. Next measure the open circuit voltage (V_T). The value of R_int is V_T/I_SC.

Example

We'll calculate and measure the values for V_T and R_int for the circuit below.

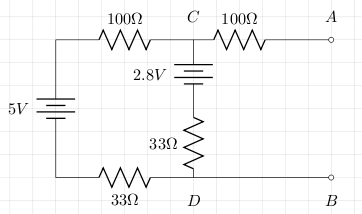
Calculation

We can use Kirchhoff's voltage law to give us the current:

5 - 2.8 = I*(100+33+33)
2.2 = I*166.
I = 2.2/166 = 0.013

Now V_T is V_CD, so:
V_T = 2.8 + 0.013*33 = 3.23

For R_int we short all voltage sources (assuming no internal resistance) and this gives the following circuit:

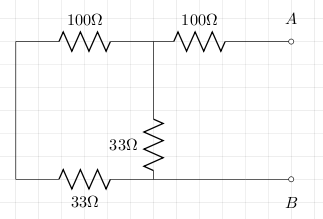
The calculation of R_int is quite easy:
R_int = 100 + 1/(1/33 + 1/133) = 100 + 26.4 = 126.4

From this we can calculate the short circuit current:
I_SC = 3.23 / 126.4 = 0.0255.

Measurement

The circuit was built and using a multimeter the value of V_T(V_CD) was 3.3V. The short circuit current I_SC was measured to be 25.6mA. From this we can calculate R_int:
R_int = 3.3/0.0256 = 128.9

Comparison

The table below shows how close the actual measurements were to the theoretical calculations.

	VT	ISC	Rint
Measured	3.3	0.0256	128.9
Calculated	3.23	0.0255	126.4

References

Fischer-Cripps. A.C., The Electronics Companion. Institute of Physics, 2005.