Resistance (AC)

Consider the following circuit:

From what we know about AC voltage, the instantaneous voltage across the resistor is

VR = V0sin(ωt)	
      

where ω is the angular frequency. If the instantaneous voltage is v, then the instantaneous current, i, is

i = v/R
  = V0sin(ωt)/R 
      

The maximum current, I₀, is when sin(ωt)=1, so

I0 = V0/R
      

So,

i = I0sin(ωt)
      

If p is instantaneous power, and P₀ is maximum power, then

p = iv
  = i2R
  = (I0sin(ωt))2R
  = I02R sin2(ωt)
P0 = I02R
p = P0sin2(ωt)
      

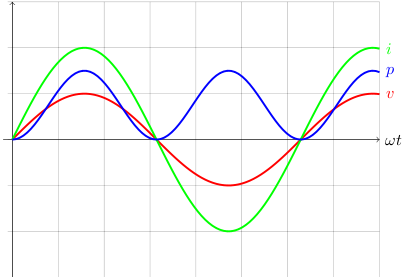
The following graph shows the relationship between the instantaneous values of voltage (v), current (i), and power (p):

References

Fischer-Cripps. A.C., The Electronics Companion. Institute of Physics, 2005.